Semi Empirical Formula For Neutrinoless Double Beta Decay
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 1798 words | ✅ Published: 09 Mar 2018 |
Abstract
A Semi empirical formula for both phase space factor and Nuclear Matrix Element (NME) is developed for neutrinoless double beta decay, and the formula is used to compute the neutrinoless double beta decay half lives. The computed half lives for neutrinoless double beta decay are compared with the corresponding experimental values and with those predicted by QRPA model. The semi empirical formula predictions are found to be in good agreement with experimental data. The semi empirical formula is used to predict neutrinoless double beta decay of various isotopes Ca, Ge, Se, Zr, Mo, Pd, Cd, Sn, Te, Xe, Nd and Sm that exhibiting single beta decay. As our semi empirical formula predictions agree with the experimental data we hope that the present work will be useful for the future experiments.
Keyword: Neutrinoless double beta decay, Nuclear Matrix Element
- Introduction
Double beta decay is a radioactive decay process where a nucleus releases two beta rays as a single process. Here two neutrons in the nucleus are converted in to two protons and in the process two electrons and two electron antineutrinos are emitted. In order for beta decay to be possible the final nucleus must have larger binding energy than the original nucleus. Double beta decay is difficult to study in most practically interesting cases, because both beta decay and double beta decay are possible, with probability favouring beta decay. The double beta decay is usually studied only for beta stable nuclei. Like single beta decay, double beta decay does not change the mass number A. More than 60 naturally occurring isotopes are capable of undergoing double beta decay.
Double beta decay is of two types; the two neutrino and neutrinoless double beta decay. The two neutrino double beta decay [2β(2ν)]  which involves the transformation of two neutrons into two protons conserves not only the electric charge but also the lepton number. On the other hand neutrinoless double beta decay [2β(0ν)]
which involves the transformation of two neutrons into two protons conserves not only the electric charge but also the lepton number. On the other hand neutrinoless double beta decay [2β(0ν)]  violates lepton number conservation and is therefore forbidden in the standard electroweak theory. According to this theory neutrinos are massless. The observation of neutrino mass and oscillation is a clear example of a phenomenon at variance with the standard model.
violates lepton number conservation and is therefore forbidden in the standard electroweak theory. According to this theory neutrinos are massless. The observation of neutrino mass and oscillation is a clear example of a phenomenon at variance with the standard model.
There are different models for explaining the double beta decay process. Among them, two methods are mainly used to calculate Nuclear Matrix Elements (NME) for 2β(0ν) decays. One is the family of Quasi particle Random Phase Approximation (QRPA) [1]. This method has been used by different groups and varieties of techniques are employed with results for most of the possible emitters [2]. The other method concerned to double beta decay process is the interacting shell model (ISM) [3]. It has been shown that as the difference in deformation between parent and daughter grows, the NME’s of both the neutrinoless and two neutrino mode decreases rapidly.
The interest in double beta decay spans more than six decades. In 1937 Racah [4] following the fundamental suggestion of Majorana [5], discussed the possibility of a neutrinoless transformation of two neutrons into two protons plus two electrons. Even earlier Geoppert-Mayer [6] evaluated the decay rate of 2β(2ν) mode and realized that the corresponding half lives could exceed 1020years. Furry [7] shortly afterwards estimated that 2β(0ν) should be much faster than 2β(2ν) decay. Thus the stage was set for the realization that observation of the 2β(0ν) decay would establish that the neutrino is a massive Majorana particle. In 1982 J. Schechter-Valle while regarding 2β(0ν) decay suggested the existence of Majorana mass of the neutrino in the frame work of Gauge theories [8]. In 1984 Fiorini et al [9] introduced a program to develop low temperature detectors for 2β decay search. Next year Doi et al [10] made a fundamental theoretical analysis of 2β decay to obtain the main formulae for probability of decay, energy and angular electron spectra. In 1986 using QRPA model Vogel et al [11] gave satisfactory agreement between theoretical and experimental 2β(2ν) half life values.
Neutrinoless double beta decay is of great interest for studying the fundamental properties of neutrino beyond the standard electro-weak theory. High sensitivity 2β(0ν) studies are the unique and practical ways for studying the Majorana nature of neutrinos, the neutrino mass spectrum, the absolute neutrino mass scale, the majorana CP phases and other fundamental properties of neutrinos in the foreseeable future. The first experiment [12] to claim 2β(0ν) is the Klapdor, HM experiment done in the year 2001. Numerous experiments like COBRA, GERDA etc have been carried out to search neutrinoless double beta decay and 48Ca, 76Ge, 82Se, 96Zr, 100Mo, 116Cd, 128Te, 150Nd, 238U are some of the isotopes exhibiting neutrinoless double beta decay [13-17].
For the double beta decay processes, two crucial ingredients are the phase space factors and the Nuclear Matrix Elements (NME). A general theory of phase space factors was developed by Doi et al. [18, 19] following the previous work of Primakoff and Rosen [20], and Konopinski [21]. It was reformulated by Tomoda [22] by approximating the electron wave functions at the nuclear radius and without inclusion of electron screening. The Nuclear Matrix Element depends on the nuclear structure of the nuclei involved in the decay. The expression for Nuclear Matrix Element can be written in general as the sum of three components [23] as
 (1)
(1)
Where ,
,  ,
,  , are the Gamow-Teller, Fermi and tensor components respectively.
, are the Gamow-Teller, Fermi and tensor components respectively.  is the axial vector coupling constant and
is the axial vector coupling constant and 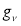 is the vector coupling constant.
is the vector coupling constant.
The present work aims to develop a semi empirical formula for both phase space factor and Nuclear Matrix Element for computing the neutrinoless double beta decay half life. By using this formula we would like to predict the possibility of 2β(0ν) decay from various isotopes exhibiting single beta decay. The details of the semi empirical formula are given in Section 2 and results, discussion and conclusion are given in Section 3.
- The semi empirical formula
In the standard scenario, when 2β(0ν) decay process occurs by exchange of light Majorana neutrinos between two nucleons inside the nucleus, and in the presence of left handed weak interactions, the life time expression can be written as a product of three factors and is given as [24]
 (2)
(2)
Where G0ν is the phase space factor for this decay mode,  is the effective neutrino mass parameter, me is the electron mass and M0ν are the Nuclear Matrix Elements depending on the nuclear structure of the nuclei involved in the decay.
is the effective neutrino mass parameter, me is the electron mass and M0ν are the Nuclear Matrix Elements depending on the nuclear structure of the nuclei involved in the decay.
The phase space factor depends on the energy decay Qββ and nuclear charge Z and studied the dependence of phase space factor with ZQ3 and Z2Q6 for various isotopes undergoing neutrinoless double beta decay. From the observed dependence of phase space factor taken from ref [25], with ZQ3 and Z2Q6 we have developed a semi empirical formula for the phase space factor. Using ZQ3, Z2Q6 and Z3Q9 as variables, a new formula is obtained and is given as,
 (3)
(3)
The constants are,  ,
, 
 ,
, 
Due to the two-body nature of the transition operator, the NMEs can also be expressed as a sum of product of two-body transition densities (TBTDs) and matrix elements of the two-body transition operators for two-particle states. We have studied the dependence of nuclear matrix element values taken from [26] with Z-1/3 for various isotopes undergoing neutrinoless double beta decay and a new formula is obtained by making least-squares fit to the nuclear matrix elements data and is given as,
 (4)
(4)
The constants are,
 ,
,  ,
, ,
,
 ,
,  ,
, 
The comparison of the computed nuclear matrix elements using the present formula with the values of Ref [26] and comparison of computed phase space factor with the values of Ref [25] are shown in Table 1.
- Results, discussion and conclusion
The Q value for double beta decay of mother nuclide with mass mm to the daughter nuclide with mass md is given by the mass difference  [27] which in turn can be written as a function of frequency ratio
[27] which in turn can be written as a function of frequency ratio  and the electron mass me;
and the electron mass me;
 (5)
(5)
In the present work Q values are computed using the experimental binding energies of Audi and Wapstra [28]. The present empirical formula is applied for all the observed neutrinoless double beta decay isotopes. Column 7 of Table 1 represents the computed half-lives for neutrinoless double beta decay of various isotopes and is compared with the experimental values given in column 8 and QRPA values [26] in column 9. It is found from the table that our formula predictions are in good agreement with the experimental values and the QRPA values. The value of
We have applied the present formula for computing the phase space factor, Nuclear Matrix Element and half lives for various isotopes that exhibiting single beta decay. Tables 2 represents the computed Q values, Phase space factors, Nuclear Matrix Elements and half lives for neutrinoless double beta decay of various Ca, Ge, Se, Zr, Mo, Pd, Cd, Sn, Te, Xe, Nd and Sm isotopes. As our semi empirical formula prediction agree with the experimental data we hope that our prediction on neutrinoless double beta decay of various Ca, Ge, Se, Zr, Mo, Pd, Cd, Sn, Te, Xe, Nd and Sm isotopes will be a guide for future experiments.
Table 1. The computed ,
,  and
and  for neutrino less double beta decay of various isotopes and their comparison with the experimental, QRPA and Ref [26] values
for neutrino less double beta decay of various isotopes and their comparison with the experimental, QRPA and Ref [26] values
_____________________________________________________________________________________
|
Isotope |
Q Value (MeV) |
_____________ |
____________ |
______________________________ |
||||
|
Present |
Ref. [ 25] |
Present |
Ref. [26] |
Present |
Expt. |
QRPA[26] |
||
_____________________________________________________________________________________
|
48Ca |
4.272 |
24.12 |
24.81 |
859.27 |
5.86E+21 |
>5.8E+22[32] |
||
|
76Ge |
2.039 |
6.44 |
2.36 |
2.90 |
2.48 |
1.93E+27 |
>1.9E+25[12] |
2.49E+27 |
|
82Se |
2.995 |
13.06 |
10.16 |
3.04 |
2.10 |
8.63E+26 |
>3.6E+23[33] |
8.13E+26 |
|
96Zr |
3.35 |
22.59 |
20.58 |
3.92 |
0.40 |
3.01E+26 |
>9.2E+21[16] |
7.70E+27 |
|
100Mo |
3.034 |
16.08 |
15.92 |
3.48 |
1.24 |
5.37E+26 |
>1.1E+24[16] |
1.45E+27 |
|
110Pd |
2.018 |
7.91 |
4.82 |
2.57 |
2.00E+27 |
|||
|
116Cd |
2.814 |
14.73 |
16.7 |
2.37 |
1.31 |
1.26E+27 |
>1.7E+23[34] |
1.13E+27 |
|
124Sn |
2.287 |
10.25 |
9.04 |
2.38 |
1.80E+27 |
|||
|
128Te |
0.866 |
1.93 |
0.59 |
2.53 |
1.47 |
8.47E+27 |
>1.5E+24[35] |
2.52E+28 |
|
130Te |
2.527 |
12.38 |
14.22 |
2.53 |
1.36 |
1.32E+27 |
>2.8E+24[17] |
1.15E+27 |
|
136Xe |
2.458 |
12.05 |
14.58 |
2.68 |
0.94 |
1.21E+27 |
>4.5E+23[36] |
2.18E+27 |
|
148Nd |
1.929 |
8.54 |
10.1 |
1.37 |
6.54E+27 |
|||
|
150Nd |
3.371 |
62.85 |
63.03 |
1.37 |
1.96 |
8.88E+26 |
>1.8E+22[37] |
1.21E+26 |
|
154Sm |
1.215 |
3.62 |
3.02 |
0.36 |
2.24E+29 |
|||
|
160Gd |
1.73 |
7.31 |
9.56 |
3.09 |
1.50E+27 |
1.30E+21[38] |
||
|
198Pt |
1.047 |
3.17 |
7.56 |
66.26 |
7.50E+24 |
_____________________________________________________________________________________
Table 2. The computed Q values, Phase space factors, nuclear matrix elements and the predicted half lives for neutrino less double beta decay of various Ca, Ge, Se, Zr, Mo, Pd, Cd, Sn, Te, Xe, Nd and Sm, Gd and Pt isotopes
____________________________________________________________
|
Isotope |
Q value (KeV) |
|
|
T1/2 (yrs) |
____________________________________________________________
|
46Ca |
988.3 |
1.58618E-15 |
859.272 |
8.92E+22 |
|
47Ca |
2592.3 |
7.53405E-15 |
859.272 |
1.88E+22 |
|
49Ca |
7269.8 |
3.40780E-12 |
859.272 |
4.15E+19 |
|
48Ca |
4273.7 |
2.41768E-14 |
859.272 |
5.85E+21 |
|
50Ca |
11855.7 |
3.44796E-10 |
859.272 |
4.10E+17 |
|
51Ca |
13867.8 |
1.44900E-09 |
859.272 |
9.76E+16 |
|
52Ca |
16955.0 |
9.01213E-09 |
859.272 |
1.57E+16 |
|
75Ge |
312.6 |
1.13809E-15 |
2.90139 |
1.09E+28 |
|
76Ge |
2039.1 |
6.44488E-15 |
2.90139 |
1.93E+27 |
|
77Ge |
3385.6 |
1.71285E-14 |
2.90139 |
7.24E+26 |
|
78Ge |
5164.1 |
5.34962E-13 |
2.90139 |
2.32E+25 |
|
79Ge |
6427.6 |
4.72938E-12 |
2.90139 |
2.62E+24 |
|
80Ge |
8244.9 |
5.07807E-11 |
2.90139 |
2.44E+23 |
|
81Ge |
10089.5 |
3.30371E-10 |
2.90139 |
3.76E+22 |
|
82Se |
2995.5 |
1.30683E-14 |
3.04409 |
8.63E+26 |
|
83Se |
4640.7 |
2.21947E-13 |
3.04409 |
5.08E+25 |
|
84Se |
6479.0 |
6.21762E-12 |
3.04409 |
1.81E+24 |
|
85Se |
9052.0 |
1.46232E-10 |
3.04409 |
7.71E+22 |
|
86Se |
12724.6 |
3.31456E-09 |
3.04409 |
3.40E+21 |
|
87Se |
14129.4 |
8.57934E-09 |
3.04409 |
1.31E+21 |
|
88Se |
15812.0 |
2.37729E-08 |
3.04409 |
4.74E+20 |
|
94Zr |
1142.9 |
2.52372E-15 |
3.91925 |
2.69E+27 |
|
95Zr |
2049.7 |
7.48180E-15 |
3.91925 |
9.09E+26 |
|
96Zr |
3347.7 |
2.25176E-14 |
3.91925 |
3.02E+26 |
|
97Zr |
4593.8 |
3.46849E-13 |
3.91925 |
1.96E+25 |
|
98Zr |
6824.7 |
1.72152E-11 |
3.91925 |
3.95E+23 |
|
99Zr |
8197.8 |
9.63615E-11 |
3.91925 |
7.06E+22 |
|
100Zr |
9584.0 |
4.08099E-10 |
3.91925 |
1.67E+22 |
|
101Zr |
10051.0 |
6.31459E-10 |
3.91925 |
1.08E+22 |
|
102Zr |
11817.0 |
2.76762E-09 |
3.91925 |
2.46E+21 |
|
103Zr |
12480.0 |
4.54642E-09 |
3.91925 |
1.50E+21 |
|
98Mo |
112.3 |
1.11526E-15 |
3.47678 |
7.75E+27 |
|
99Mo |
1651.2 |
5.10021E-15 |
3.47678 |
1.69E+27 |
|
100Mo |
3035.0 |
1.60950E-14 |
3.47678 |
5.37E+26 |
|
101Mo |
4438.7 |
2.88638E-13 |
3.47678 |
2.99E+25 |
|
102Mo |
5541.0 |
2.68528E-12 |
3.47678 |
3.22E+24 |
_____________________________________________________________
Table 2. Continued…..
____________________________________________________________
|
Isotope |
Q value (KeV) |
|
|
T1/2 (yrs) |
____________________________________________________________
|
103Mo |
6408.8 |
1.10330E-11 |
3.47678 |
7.83E+23 |
|
104Mo |
7759.0 |
6.71620E-11 |
3.47678 |
1.29E+23 |
|
105Mo |
8588.0 |
1.72446E-10 |
3.47678 |
5.01E+22 |
|
106Mo |
10067 |
7.43636E-10 |
3.47678 |
1.16E+22 |
|
107Mo |
11430 |
2.37009E-09 |
3.47678 |
3.65E+21 |
|
109Pd |
901.0 |
1.92669E-15 |
2.56879 |
8.22E+27 |
|
110Pd |
2004.0 |
7.81588E-15 |
2.56879 |
2.03E+27 |
|
111Pd |
3253.5 |
2.48567E-14 |
2.56879 |
6.37E+26 |
|
112Pd |
4244.5 |
2.49383E-13 |
2.56879 |
6.35E+25 |
|
113Pd |
5359.3 |
2.60657E-12 |
2.56879 |
6.07E+24 |
|
114Pd |
6523.9 |
1.74643E-11 |
2.56879 |
9.06E+23 |
|
115Pd |
7690.5 |
8.20373E-11 |
2.56879 |
1.93E+23 |
|
116Pd |
8759.0 |
2.73683E-10 |
2.56879 |
5.78E+22 |
|
117Pd |
9895.0 |
8.38279E-10 |
2.56879 |
1.89E+22 |
|
118Pd |
11239 |
2.67934E-09 |
2.56879 |
5.91E+21 |
|
114Cd |
540.1 |
1.30076E-15 |
2.37189 |
1.43E+28 |
|
115Cd |
1945.5 |
7.60027E-15 |
2.37189 |
2.44E+27 |
|
116Cd |
2809.1 |
1.46594E-14 |
2.37189 |
1.27E+27 |
|
117Cd |
3975.0 |
1.46594E-14 |
2.37189 |
1.25E+26 |
|
118Cd |
4947.1 |
1.48733E-13 |
2.37189 |
1.37E+25 |
|
119Cd |
6158.4 |
1.35555E-12 |
2.37189 |
1.61E+24 |
|
120Cd |
7131.1 |
1.15360E-11 |
2.37189 |
4.01E+23 |
|
121Cd |
8144.1 |
4.62494E-11 |
2.37189 |
1.17E+23 |
|
122Cd |
9215.9 |
1.59314E-10 |
2.37189 |
3.73E+22 |
|
123Cd |
10510.5 |
4.97662E-10 |
2.37189 |
1.12E+22 |
|
124Cd |
11526.8 |
1.65584E-09 |
2.37189 |
4.84E+2 |
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal



