Definition of SETS, Union, Intersection and Complement
| ✅ Paper Type: Free Essay | ✅ Subject: Information Technology |
| ✅ Wordcount: 778 words | ✅ Published: 20 Sep 2017 |
Benjamin Quarshie
Section A – Assignment Information
Set Theory
- Explain the following terms:
SETS
The word “set” is generally associated with the idea of grouping objects, such as a set of records, books, crop plants and other words such as herd, herd, herd, plots, peasantry, family, etc. Saying the word set denotes a collection of elements clearly between them, which keep some characteristic in common. Be it numbers, people, figures, ideas and concepts.
In math, the concept of a set is considered primitive and does not give a definition of it, but rather works with the notation of collection and grouping of objects, so it may be said that the ideas of element and belonging are considered primitive.
The essential characteristic of a set is to be well defined, i.e. given a particular object, to determine whether or not it belongs to the set. For example, if we consider the set of digit numbers, we know that 3 belong to the set, but 19 do not. On the other hand the set of beautiful musical works is not a well defined set, since different people can include different works in the set.
Objects that form a set are called members or elements. For example the set of letters of alphabet; A b c … x, y, z which can be written like this:
Example of two sets, A and B:
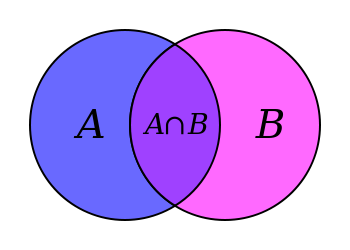
UNION
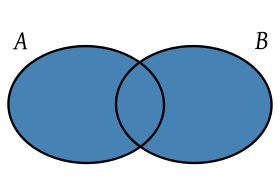
The union of sets corresponds to the unification of the elements of two conjuncts or even more sets, which may from this constitute a new form of set, in which the elements within it correspond to the elements of the original sets. When an element is repeated, it forms part of the union set once only; This differs from the union of sets in the traditional conception of addition, in which common elements are considered as many times as they are in the totality of sets. We can say that the union of sets is a binary operation (that mathematical operation, which requires the operator and two arguments to be able to calculate a value) in the set of all subsets of a U, Universal Set consisting of all elements of the reference theme) given. By which each pair of sets A and B of U is associated with another set (A U B) of U. If A and B are two sets, the union is defined as follows:
INTERSECTION
The Intersection of two or more sets is the set formed by the elements that have in common both sets. The intersection of A and B is denoted. In diagrams all the elements in their respective sets are first represented and then the zone belonging to both sets is coloured.

COMPLEMENT
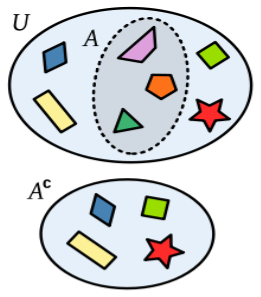
The complement of a complementary set or set is another set that contains all elements that are not in the original set. In order to define it, it is necessary to specify what type of elements are being used, or otherwise, what the universal set is. For example, if one speaks of natural numbers, the complement of the set of prime numbers P is the set of non-prime numbers C, which is composed of the compound numbers and the 1:
UNIVERSAL SET
This is called the set that contains all the elements. This set depends on the problem being studied, is a set whose object of study are the subsets of it. Primarily the universal whole was considered as the set of all things, but at present it is proved that this set does not exist. At the present time it should be made clear which set is being treated. If we treat sets whose elements are letters, the universal set would be the one that was formed by all the letters of the alphabet. The complement of the universe (or referential) set is the empty set. The universal set is indicated by the letter U and sometimes indicated by the letter S.
POWER SET
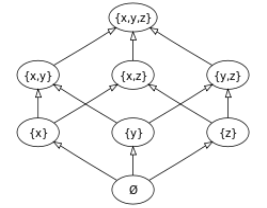
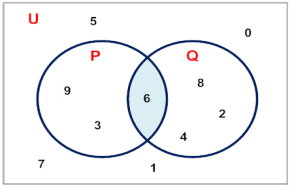
2.5 Venn Diagrams
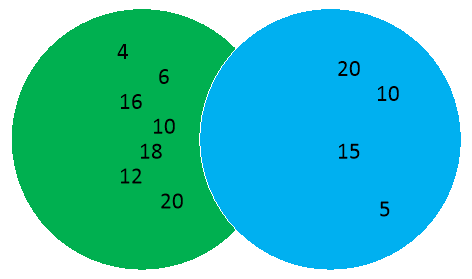
SET A (EVEN NUMBERS) SET B (NUMBERS DIVISIBLE BY 5)


- Show the 2 sets using bracket notation
SET A = {2,4,6,8,10,12,14,16,18,20}
SET B = {5,10,15,20,25,30}


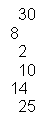

2.2 The union of set A and set B are listed below:
A U B = {2,4,5,6,8,10,12,14,15,16,18,20,25,30}
2.2 The intersection of Set A and Set B


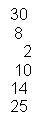

A n B = {30,8,2,10,14,25}
2.3 The Complement of Set A

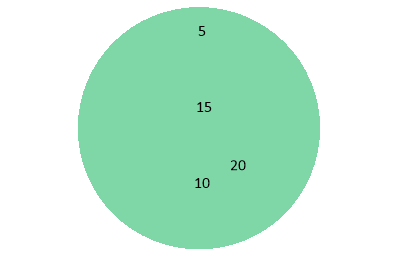
- d) D is the set of dogs which includes the following subsets – B (the set of Boxers), L (the set of Labradors) and P (the set of Poodles). Express the power set of D using bracket notation.



 SET B
SET B





 SET P
SET P
SET L
References
Webpage [http://study.com/academy/lesson/union-of-sets-in-math-definition-terms-symbol.html] Accessed on [24/02/2017]
Webpage [https://www.reference.com/math/well-defined-set-mathematics-4895437ff1cbabd9] Accessed on [24/02/2017]
Webpage [http://searchsecurity.techtarget.com/definition/set] Accessed on [27/02/2017]
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal



