Comparative Analysis of Rank Techniques
| ✅ Paper Type: Free Essay | ✅ Subject: Computer Science |
| ✅ Wordcount: 2690 words | ✅ Published: 22 Jun 2018 |
Abstract
There is paramount web data available in the form of web pages on the World Wide Web (WWW). So whenever a user makes a query, a lot of search results having different web links corresponding to a user’s query are generated. Out of which only some are relevant while the rest are irrelevant. The relevancy of a web page is calculated by search engines using page ranking algorithms. Most of the page ranking algorithm use web structure mining and web content mining to calculate the relevancy of a web page. Most of the ranking algorithms which are given in the literature are either link or content oriented which do not consider user usage trends. The Algorithm called Page Rank Algorithm was introduced by Google in beginning. It was considered a standard page rank because as no other algorithm of page rank was in existence. Later extensions of page rank algorithm were incorporated along with different variations like considering weights as well as visits of links. This paper presents the comparison among original page rank algorithm as well as its various variations.
Keywords: inlinks, outlinks, search engine, web mining, World Wide Web (WWW), PageRank, Weighted page rank, VOL
I. Introduction
World Wide Web is a vast resource of hyperlinked and a variety of information including text, image, audio, video and metadata. It is anticipated that WWW has expanded by about 2000% since its progression and is doubling in magnitude with a gap of six to ten months. With the swift expansion of information on the WWW and mounting requirements of users, it is becoming complicated to manage web information and comply with the user needs. So users have to employ some information retrieval techniques to find, extract, filter and order the desired information. The technique used filters the web page according to query generated by the user and create an index. This indexing is related to the rank of web page. Lower the index value, higher will be the rank of the web page.
1. Data Mining over Web
1.1 Web Mining
Data mining, which facilitates the knowledge discovery from large data sets by extracting potentially new useful patterns in the form of human understandable knowledge and structuring the same, can also be applied over the web. The application being named Web Mining thus becomes a technique for extracting useful information from a large, unstructured, heterogeneous data store. Web mining is quite a immense area with dozens of developments and technological enhancements.
1.2. Web Mining Categories
According to literature, there are three categories of web mining: Web Content Mining (WCM), Web Structure Mining (WSM) and Web Usage Mining (WUM)
WCM includes the web page information. In it, the actual content pages whether semi structured hypertext or multimedia information are used for searching purposes.
WSM uses the central part linkage that flows through the entire web. The linkage of web content is called hyperlink. This hyperlinked structure is used for ranking the retrieved web pages on the basis of query generated by the user.
WUM returns the dynamic results with respect to users’ navigation. This methodology uses the server logs ( the logs that are created during user navigation via searching. WUM is also called as Web Log Mining because it extracts knowledge from usage logs.
1.2 Page Rank Algorithm (By Google)
This is the original PageRank algorithm. It was postulated by Lawrence Page and Sergey Brin. The formula is:

where

 is the PageRank of page A
is the PageRank of page A

 is the PageRank of pages Ti which link to page A
is the PageRank of pages Ti which link to page A

 is the number of outbound links on page Ti
is the number of outbound links on page Ti
 d is a damping factor having value between 0 and 1.
d is a damping factor having value between 0 and 1.
The PageRank algorithm is used to determine the rank of a web page individually. This algorithm is not meant to rank a web site. Moreover, the PageRank of a page say A, is recursively defined by the PageRanks of those pages which link to page A. The PageRank of pages  which link to page A does not influence the PageRank of page A consistently. In PageRank algorithm, the PageRank of a page T is always weighted by the number of outbound links C(T) on page T. It means, more outbound links a page T has, the less will page A benefit from a link to it on page T. The weighted PageRank of pages Ti is then added up. But an additional inbound link for page A will always increase page A’s PageRank. In the end, the sum of the weighted PageRanks of all pages
which link to page A does not influence the PageRank of page A consistently. In PageRank algorithm, the PageRank of a page T is always weighted by the number of outbound links C(T) on page T. It means, more outbound links a page T has, the less will page A benefit from a link to it on page T. The weighted PageRank of pages Ti is then added up. But an additional inbound link for page A will always increase page A’s PageRank. In the end, the sum of the weighted PageRanks of all pages  is multiplied with a damping factor d which can be set between 0 and 1. Thus, the extend of PageRank benefit for a page by another page linking to it is reduced.
is multiplied with a damping factor d which can be set between 0 and 1. Thus, the extend of PageRank benefit for a page by another page linking to it is reduced.
They deem PageRank as a genre of user behaviour, where a surfer clicks on links at random irrespective of content. The random surfer visits a web page with a certain probability which is solely given by the number of links on that page. Thus, one page’s PageRank is not completely passed on to a page it links to, but is divided by the number of links on the page. So, the probability for the random surfer reaching one page is the sum of probabilities for the random surfer following links to this page. Now, this probability is diminish by the damping factor d. Sometimes, user doesnot move straight to the links of a page, instead the user jumps to some other page randomly. This probability for the random surfer is calculated by the damping factor d (also called as degree of probability having value between 0 and 1). Regardless of inbound links, the probability for the random surfer jumping to a page is always (1-d), so a page has always a minimum PageRank.
A revised version of the PageRank Algorithm is given by Lawrence Page and Sergey Brin. In this algorithm, the PageRank of page A is given as

where N is the total number of all pages on the web. This revised version of the algorithm is basically equivalent the original one. Regarding the Random Surfer Model, this version is the actual probability for a surfer reaching that page after clicking on many links. The sum of all page ranks of all pages will be one by calculating the probability distribution of all web pages.
But, these versions of the algorithm do not differ fundamentally from each other. A PageRank which has been calculated by using the second version of the algorithm has to be multiplied by the total number of web pages to get the according PageRank that would have been calculated by using the first version.
1.3 Dangling Nodes
A node is called a dangling node if it does not contain any out-going link, i.e., if the out-degree is zero. The hypothetical web graph taken in this paper is having a dangling node i.e. Node D.
II Research background
Brin and Page (Algorithm: Google Page Rank)
The authors came up with an idea to use link structure of the web to calculate rank of web pages. This algorithm is used by Google based on the results produced by keyword based search. It works on the principle that if a web page has significant links towards it, then the links of this page to other pages are also considered imperative. Thus, it depends on the backlinks to calculate the rank of web pages. The page rank is calculated by the formula given in equation 1.
 (1)
(1)
Where
u represents a web page
 and
and  represents the page rank of web pages u and v respectively
represents the page rank of web pages u and v respectively
 is the set of web pages pointing to u
is the set of web pages pointing to u
 represents the total numbers of outlinks of web page
represents the total numbers of outlinks of web page
v and c is a factor used for normalization
Original PageRank algorithm was modified considering that all users donot follow direct links on web data. Thus, the modified formula for calculating page rank is given in equation 2.
 (2)
(2)
Where
d is a dampening factor which represent the probability of user using direct links and it can be set between 0 and 1.
Wenpu Xing and Ali Ghorbani (Algorithm: Weighted Page Rank)
The authors gave this method by extending standard PageRank. It works on the theory that if a page is vital, it has many inlinks and outlinks. Unlike standard PageRank, it does not equally distribute the page rank of a page among its outgoing linked pages. The page rank of a web page is divided among its outgoing linked pages in proportional to the importance or popularity (its number of inlinks and outlinks).
 , the popularity from the number of inlinks, is calculated based on the number of inlinks of page u and the number of inlinks of all reference pages of page v as given in equation 3.
, the popularity from the number of inlinks, is calculated based on the number of inlinks of page u and the number of inlinks of all reference pages of page v as given in equation 3.
 (3)
(3)
Where  and
and  are the number of inlinks of page u and p respectively
are the number of inlinks of page u and p respectively
 represents the set of web pages pointed by v.
represents the set of web pages pointed by v.
 , the popularity from the number of outlinks, is calculated based on the number of outlinks
, the popularity from the number of outlinks, is calculated based on the number of outlinks
of page u and the number of outlinks of all reference pages of page v as given in equation. 4.
 (4)
(4)
Where  and
and  are the number of outlinks of page u and p respectively
are the number of outlinks of page u and p respectively
 represents the set of web pages pointed by v.
represents the set of web pages pointed by v.
The page rank using Weighted PageRank algorithm is calculated by the formula as given in equation 5.
 (5)
(5)
Gyanendra Kumar et. al. (Algorithm : Page Rank with Visits of Links (VOL))
This methodology includes the browsing behavior of the user. The prior algorithms were either based on WSM or WCM. But it incluses Page Ranking based on Visits of Links (VOL). It modifies the basic page ranking algorithm by considering the number of visits of inbound links of web pages. It assists to prioritize the web pages on the basis of user’s browsing behavior. Also, the rank values are assigned in proportional to the number of visits of links in this algorithm. The more rank value is assigned to the link which is most visited by user. The Page Ranking based on Visits of Links (VOL) can be calculated by the formula given in equation 6.
 (6)
(6)
Where
 and
and  represent page rank of web pages u and v respectively
represent page rank of web pages u and v respectively
d is dampening factor
B(u) is the set of web pages pointing to u
Lu is number of visits of links pointing from v to u
TL(v) is the total number of visits of all links from v.
Neelam Tyagi and Simple Sharma (Algorithm: Weighted Page Rank Algorithm Based on Number of Visits of Links of Web Page)
The authors incorporate Weighted PageRank algorithm and the number of visits of links (VOL). This algorithm consigns more rank to the outgoing links having high VOL. It is based on the inlink popularity ignoring the outlink popularity. In this algorithm, number of visits of inbound links of web pages are taken into consideration in addition the weights of page. The rank of web page using this algorithm can be calculated as given in equation 7.
 (7)
(7)
Where
 represent page rank of web page u and v respectively
represent page rank of web page u and v respectively
d is the dampening factor
B(u) is the set of web pages pointing to u
Lu is number of visits of links pointing from v to u
 is the total number of visits of all links from v
is the total number of visits of all links from v
 represents the popularity from the number of inlinks of u.
represents the popularity from the number of inlinks of u.
Sonal Tuteja (Algorithm: Enhancement in Weighted Page Rank Using Visits of Link (VOL))
The author incorporated  i.e. the weight of link(v,u) and calculated based on the number of visits of inlinks of page u.
i.e. the weight of link(v,u) and calculated based on the number of visits of inlinks of page u.
 the popularity from the number of visits of outlinks are used to calculate the value of page rank.
the popularity from the number of visits of outlinks are used to calculate the value of page rank.
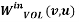 is the weight of link(v, u) which is calculated based on the number of visits of inlinks of page u and the number of visits of inlinks of all reference pages of page v as given in equation 8.
is the weight of link(v, u) which is calculated based on the number of visits of inlinks of page u and the number of visits of inlinks of all reference pages of page v as given in equation 8.
 (8)
(8)
Where
 and
and  represents the incoming visits of links of page u and p respectively
represents the incoming visits of links of page u and p respectively
R(v) represents the set of reference pages of page v.
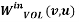 is the weight of link(v, u) which is calculated based on the number of visits of outlinks of page u and the number of visits of outlinks of all reference pages of page v as given in equation 9.
is the weight of link(v, u) which is calculated based on the number of visits of outlinks of page u and the number of visits of outlinks of all reference pages of page v as given in equation 9.
 (9)
(9)
Where  and
and  represents the outgoing visits of links of page u and v respectively
represents the outgoing visits of links of page u and v respectively
R(v) represents the set of reference pages of page v.
Now these values are used to calculate page rank using equation (10)
 (10)
(10)
Where
d is a dampening factor
B(u) is the set of pages that point to u
WPRVOL (u) and WPRVOL(v) are the rank scores of page u and v respectively
 represents the popularity from the number of visits of inlinks
represents the popularity from the number of visits of inlinks
 represents the popularity from the number of visits of outlinks
represents the popularity from the number of visits of outlinks
III Numerical analysis of various page rank algorithms
To demonstrate the working of page rank, consider a hypothetical web structure as shown below:







Figure showing a web graph having three web pages i.e. A, B, C, D
- Page Rank (By Brin & Page)
Using equation 2, the ranks for pages A, B, C are calculated as follows:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
Having value d=0.25, 0.5, 0.85, the page ranks of pages A, B and C become:
|
Dampening Factor |
PR(A) |
PR(B) |
PR(C) |
PR(D) |
|
0.25 |
0.9 |
0.975 |
1.22 |
0.99 |
|
0.5 |
0.8 |
0.9 |
1.35 |
0.95 |
|
0.85 |
0.85 |
0.829 |
1.53 |
0.357 |
From the results, it is concluded that
PR(C)> PR(D)> PR(B)> PR(A)
2. Iterative Method of Page Rank
It is easy to solve the equation system, to determine page rank values, for a small set of pages, but the web consists of billions of documents and it is not possible to find a solution by inspection method. In iterative calculation, each page is assigned a starting page rank value of 1 as shown in table 1 below. These rank values are iteratively substituted in page rank equations to find the final values. In general, many iterations could be followed to normalize the page ranks.
|
d=0.25 |
d=0.5 |
d=0.85 |
||||||||||
|
Iteration |
PR(A) |
PR(B) |
PR(C) |
PR(D) |
PR(A) |
PR(B) |
PR(C) |
PR(D) |
PR(A) |
PR(B) |
PR(C) |
PR(D) |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1.25 |
1 |
1 |
1 |
1.5 |
1 |
1 |
0.5 |
1.425 |
0.575 |
|
2 |
0.875 |
0.97 |
1.21 |
0.99 |
0.875 |
0.94 |
1.44 |
0.97 |
0.75 |
0.788 |
1.46 |
0.82 |
|
3 |
0.90 |
0.975 |
1.22 |
0.99 |
0.86 |
0.93 |
1.4 |
0.965 |
0.77 |
0.80 |
1.48 |
0.83 |
|
——— |
—— |
—— |
—— |
…… |
…… |
……. |
…… |
…… |
…… |
…… |
…… |
……. |
From the results, it is concluded that
PR(C)> PR(D)> PR(B)> PR(A)
3. Page Rank with Visits of Links (VOL) (Gyanendra Kumar)
Using equation 6, the ranks for pages A, B, C are calculated as follows:
 (A)=(1-d)+d(
(A)=(1-d)+d( (1)
(1)
 (B)=(1-d)+d(
(B)=(1-d)+d( (2)
(2)
 (C)=(1-d)+d(
(C)=(1-d)+d( +
+ (3)
(3)
 (D)=(1-d)+d(
(D)=(1-d)+d( (4)
(4)
The intermediate values can be calculated as:

Similarly other values after calculation are:

 2/3
2/3


Having value d=0.25,0.5, 0.85 the page ranks of pages A, B and C become:
|
Dampening Factor |
PR(A) |
PR(B) |
PR(C) |
PR(D) |
|
0.25 |
0.83 |
0.82 |
1.23 |
0.818 |
|
0.5 |
0.635 |
0.606 |
0.808 |
0.6 |
|
0.85 |
0.2478 |
0.22 |
0.3449 |
0.1123 |
From the results, it is concluded that
PR(C)> PR(A)> PR(B)> PR(D)
4. Weighted Page Rank (Wenpu Xing and Ali Ghorbani)
Using equation 3, the ranks for pages A, B, C are calculated as follows:
 (C,A).
(C,A). (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
The weights of incoming as well as well as outgoing links can be calculated as:
 (C,A)= IA/IA+IC = 1/ 1+2 = 1/3
(C,A)= IA/IA+IC = 1/ 1+2 = 1/3
 =OA/OA=1
=OA/OA=1
Having value d=0.5, the page ranks of pages A, B and C become:
|
Dampening Factor |
PR(A) |
PR(B) |
PR(C) |
PR(D) |
|
0.25 |
0.8526 |
0.8210 |
1.2315 |
0.75 |
|
0.5 |
0.7059 |
0.6176 |
1.235 |
0.5 |
|
0.85 |
0.3380 |
0.2458 |
0.6636 |
0.15 |
From the results, it is concluded that
PR(C)> PR(A)> PR(B)> PR(D)
5. Weighted Page Rank Based on Visits of Link (VOL) (Neelam Tyagi and Simple Sharma)
Using equation 7, the ranks for pages A, B, C are calculated as follows:
 )(1)
)(1)
 )(2)
)(2)
 (3)
(3)
 (4)
(4)
The weights of incoming, number of visits of link as well as total number of visits of all links can be calculated as

Having value d=0.25, 0.5 & 0.85, the page ranks of pages A, B and C become:
|
Dampening Factor |
PR(A) |
PR(B) |
PR(C) |
PR(D) |
|
0.25 |
0.8061 |
0.7836 |
1.015 |
0.8153 |
|
0.5 |
05981 |
0.5498 |
0.8825 |
0.5916 |
|
0.85 |
0.1734 |
0.1735 |
0.3469 |
0.1994 |
From the results, it is concluded that
PR(C)> PR(D)> PR(A)> PR(B)
5. Enhancement in Weighted Page Rank Using Visits of Link (VOL) (Sonal Tuteja)
Using equation 10, the ranks for pages A, B, C are calculated as follows:
 (1)
(1)
 (2)
(2)
 (3)
(3)

Intermediate values can be calculated as follows:
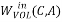 =IA/IA=1
=IA/IA=1
 =OA/OA=1
=OA/OA=1
Having value d=0.25, 0.5, 0.85 the page ranks of pages A, B and C become:
|
Dampening Factor |
PR(A) |
PR(B) |
PR(C) |
PR(D) |
|
0.25 |
0.7226 |
0.7951 |
1.029 |
0.75 |
|
0.5 |
0.9557 |
0.6195 |
0.9115 |
0.5 |
|
0.85 |
1.911 |
0.5561 |
1.116 |
0.15 |
From the results, it is concluded that
PR(C)> PR(B)> PR(D)> PR(A)
Comparison chart of various Ranking Algorithms
|
Algorithm |
Page Rank |
Page Rank with VOL |
Weighted Page rank |
WPRV |
EWPRV |
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal



